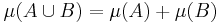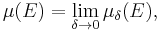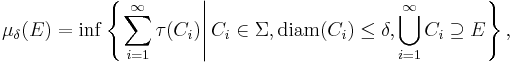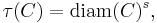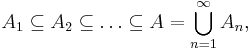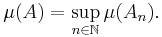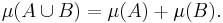Metric outer measure

In mathematics, a metric outer measure is an outer measure μ defined on the subsets of a given metric space (X, d) such that

$\mu (A \cup B) = \mu (A) %2B \mu (B)$

for every pair of positively separated subsets A and B of X.

Construction of metric outer measures

Let τ : Σ → [0, +∞] be a pre-measure on X, i.e. a set function defined on a class Σ of subsets of X containing the empty set ∅, such that τ(∅) = 0. One can show that the set function μ defined by

$\mu (E) = \lim_{\delta \to 0} \mu_{\delta} (E),$

where

$\mu_{\delta} (E) = \inf \left\{ \left. \sum_{i = 1}^{\infty} \tau (C_{i}) \right| C_{i} \in \Sigma, \mathrm{diam} (C_{i}) \leq \delta, \bigcup_{i = 1}^{\infty} C_{i} \supseteq E \right\},$

is not only an outer measure, but in fact a metric outer measure as well. (Some authors prefer to take a supremum over δ > 0 rather than a limit as δ → 0; the two give the same result, since μ_δ(E) increases as δ decreases.)

For the function τ one can use

$\tau(C) = \mathrm{diam} (C)^s,\,$

where s is a positive constant; this τ is defined on the power set of all subsets of X; the associated measure μ is the s-dimensional Hausdorff measure. More generally, one could use any so-called dimension function.

This construction is very important in fractal geometry, since this is how the Hausdorff and packing measures are obtained.

Properties of metric outer measures

Let μ be a metric outer measure on a metric space (X, d).

For any sequence of subsets A_n, n ∈ N, of X with

$A_{1} \subseteq A_{2} \subseteq \dots \subseteq A = \bigcup_{n = 1}^{\infty} A_{n},$

and such that A_n and A \ A_n+1 are positively separated, it follows that

$\mu (A) = \sup_{n \in \mathbb{N}} \mu (A_{n}).$

All the d-closed subsets E of X are μ-measurable in the sense that they satisfy the following version of Carathéodory's criterion: for all sets A and B with A ⊆ E and B ⊆ X \ E,

$\mu (A \cup B) = \mu (A) %2B \mu (B).$

Consequently, all the Borel subsets of X — those obtainable as countable unions, intersections and set-theoretic differences of open/closed sets — are μ-measurable.

References

Rogers, C. A. (1998). Hausdorff measures. Cambridge Mathematical Library (Third ed.). Cambridge: Cambridge University Press. pp. xxx+195. ISBN 0-521-62491-6.